2016bctf带OLLVM混淆的LostFlower题解

前言

第一次分析so层混淆的程序，ollvm真的是个神器。最先我还天真地看了半天汇编，ollvm可以让你分析时间翻几十倍。我并没有找到任何方法来抵抗这种混淆的方法，所以要分析只有硬刚。我先整理了一下网上关于ollvm的描述，然后根据我自己分析过程给出一些自己的理解。最后写了一下2016bctf的LostFlower的题解。

ollvm简介

ollvm是对于so层函数，c语言函数混淆的方法。之前在java层遇到过诸如proguard的一些混淆，但是大家对于他们的评价都是这种混淆只是混乱了一下逻辑，并没有什么作用，让分析时间增多，也只是略微增多一点。但是我想说ollvm是让人绝望地增多，当然也可能是我第一次接触这个东西。原本好好的代码经过ollvm处理后的结果就是这样的

1

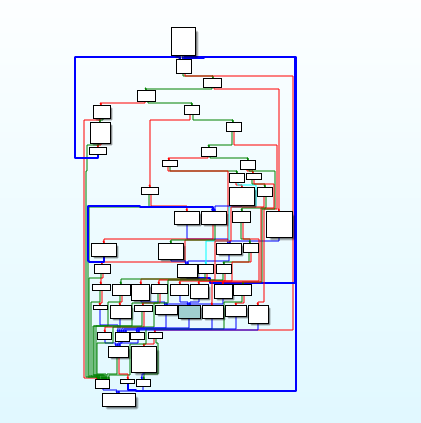
具体原理（网上找的）：正常的求和代码

2

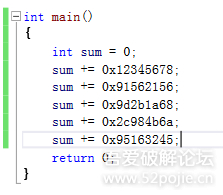
复杂一点的表达方式：

3

再复杂一点的表达方式：

4

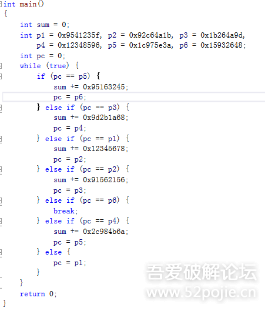
​ 可以看到，函数执行的流程不再是由上到下的顺序流了，而是根据pc的值，动态得选择if块中的语句执行，同时把下一个if块的地址赋予pc指针，这个就是OLLVM大概的思路。

​ 在做bctf这道题时，总结出ollvm的套路：定义一个变量，并不断使用这个变量，对他赋值对他大小进行比较、跳转。然后在这中间加入我们程序中真正有用的逻辑。我们在进行分析的时候需要不断地跟踪这个变量，一般来说这个变量是不会改变的。然后在中间找到代码真正的逻辑，由于代码不停的上下跳转也很难定到一个地方让他执行到这一步。所以我们需要特别仔细，特别关注if语句中判断是否相等条件下进行的处理。

LostFlower

打开这道题还是第一步扔到jeb中查看

5

逻辑很简单，将输入变为double类型，然后将这个值使用so中的stringFromJNI进行处理，返回结果如果等于6，那么就可以直接处理过后生成flag。ida打开so文件，由于没有什么反调试的措施，所以我们直接上动态调试。

跳过一堆判断函数后，找到了处理的关键check1函数，参数是我们输入数字的整数部分，我想吐槽，正常人会输小数？进入该函数后，又是一大堆烦人的跳转，我们从返回值逆向回去，也可以一步一步地走来看。其实在进行了几步后我们就可以看到他的规律，程序通过v2这个变量也就是我们寄存器r0的值，不断用它进行大于小于、等于不等于的比较，跳转到不同逻辑，有一些逻辑不涉及到改变v2的值，所以不会影响整个程序的流程，重点关注对v2进行赋值的代码。下面通过一整个循环大家就清楚了

6

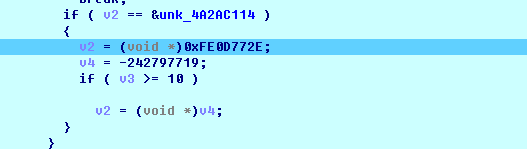
判断v2是否等于4A2AC114，等于赋值FE0D772E给他

7

8

9

10

11

12

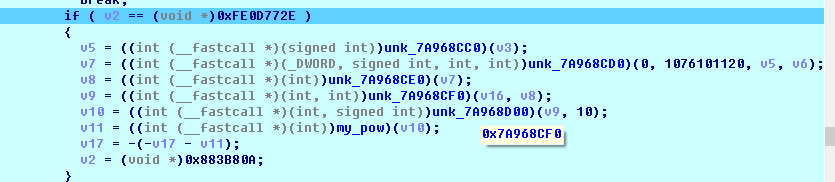
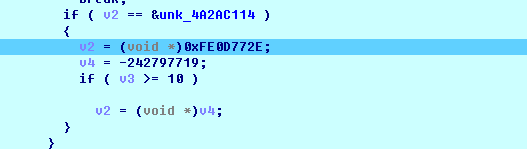
关键代码如上，就跟我们分析的一样关键是看v2的值的跳转，我们理清里边包含的逻辑，就是每一轮对v3进行加1，一共加到10，每一次循环都执行第一张图的处理，我们来分析这段代码的处理：

1
2
3
4
5
6
7
8
v5 = j_j___aeabi_i2d(v3);
v7 = j_j_pow_0(0, 1076101120, v5, v6);
v9 = j_j___aeabi_d2iz(v7, v8);
v10 = j_j___aeabi_idiv(v17, v9);
v11 = j_j___modsi3(v10, 10);
v12 = my_pow(v11);
v18 = -(-v18 - v12);
v2 = (void *)142850058;

这里几个函数都是一些除法、求余的操作。经过几轮动态调试，事实上，这个for循环的前五行代码就是逆向取出一个10位整数的每一位。举个例子，输入为1234567890，每一轮得到的依次为0，9，8，7，6，5，4，3，2，1。

现在还剩下一个 my_pow,顾名思义这是个幂相关的函数。注意我们不需要去具体分析 my_pow,因为我们的输入只有0-9这10种可能，几轮测试过后，得到结论：my_pow返回输入数据的十次幂。

用C代码重现下这个for循环：

1
2
3
4
5
6
7
8
9
10
11
int i;
int integer; // 用户输入的整数部分
int out;    // 即v12
out = 0;
for (i = 0; i < 10; ++i) {
    int x;
    
    x = integer / pow(10, i) % 10;
    out += pwo(x, 10);
}

继续执行：

13

14

15

16

17

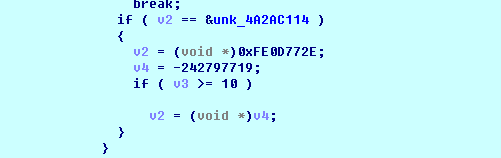
sub_7A965AA4，计算括号内的值，为负补之返回，不为负则直接返回

18

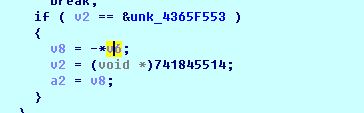
继续看主函数，需要返回负值，并且输入大于1000000000，则输出为6。由于逻辑太复杂，所以简单点的方法是直接修改返回值，可以看到这两个就是最终的判断条件，其他地方再没有任何有用的判断代码了。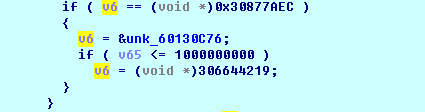19

所以关键在于我们要让之前的sub_7A965AA4返回负值。通过对sub_1AA4的汇编代码的分析，发现了溢出点：NEGS R1, R1。其中 NEGS 的作用是这样的：将目的操作数的所有数据位取反加1。当参数为0x80000000（负的2^31，最小的负数）时，所有数据位取反后为0x8fffffff，再加1后发生溢出，最后值为0x80000000。

解密代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
int main()
{
	int pow_table[] = {0, 1, 0x400, 0xe6a9, 0x100000, 0x9502f9, 0x39aa400, 0x10d63af1, 0x40000000, 0xcfd41b91};
	int i;
	for (i = 1000000000; i <= 0x80000000; ++i) {
		int a0 = i % 10;
		int a1 = (i % 100) / 10;
		int a2 = (i % 1000) / 100;
		int a3 = (i % 10000) / 1000;
		int a4 = (i % 100000) / 10000;
		int a5 = (i % 1000000) / 100000;
		int a6 = (i % 10000000) / 1000000;
		int a7 = (i % 100000000) / 10000000;
		int a8 = (i % 1000000000) / 100000000;
		int a9 = i / 1000000000;
		
		int sum = pow_table[a0] + pow_table[a1] + pow_table[a2] + pow_table[a3] + pow_table[a4] + pow_table[a5] + pow_table[a6] + pow_table[a7] + pow_table[a8] + pow_table[a9];
		if (((i - sum) & 0xffffffff) == 0x80000000) 
		{
			printf("ok, %d\n", i);
			break;
		}
		if(i % 1000000 == 0)
		{
			printf("%d\n",i);
		}
	}
	return 0;
}

输入为1422445956，Flag为BCTF{wrhav3f4nwxo}。

Comments

⬆︎TOP